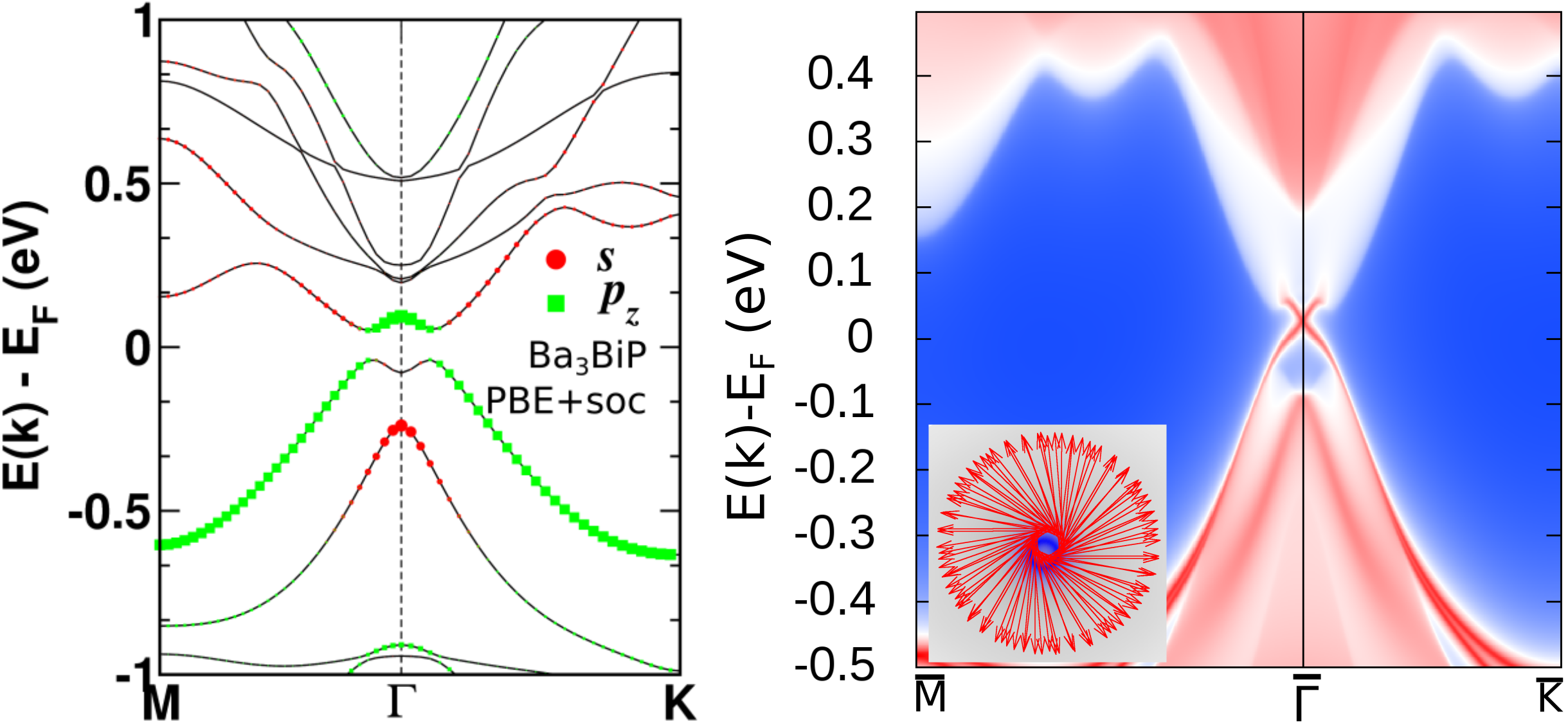
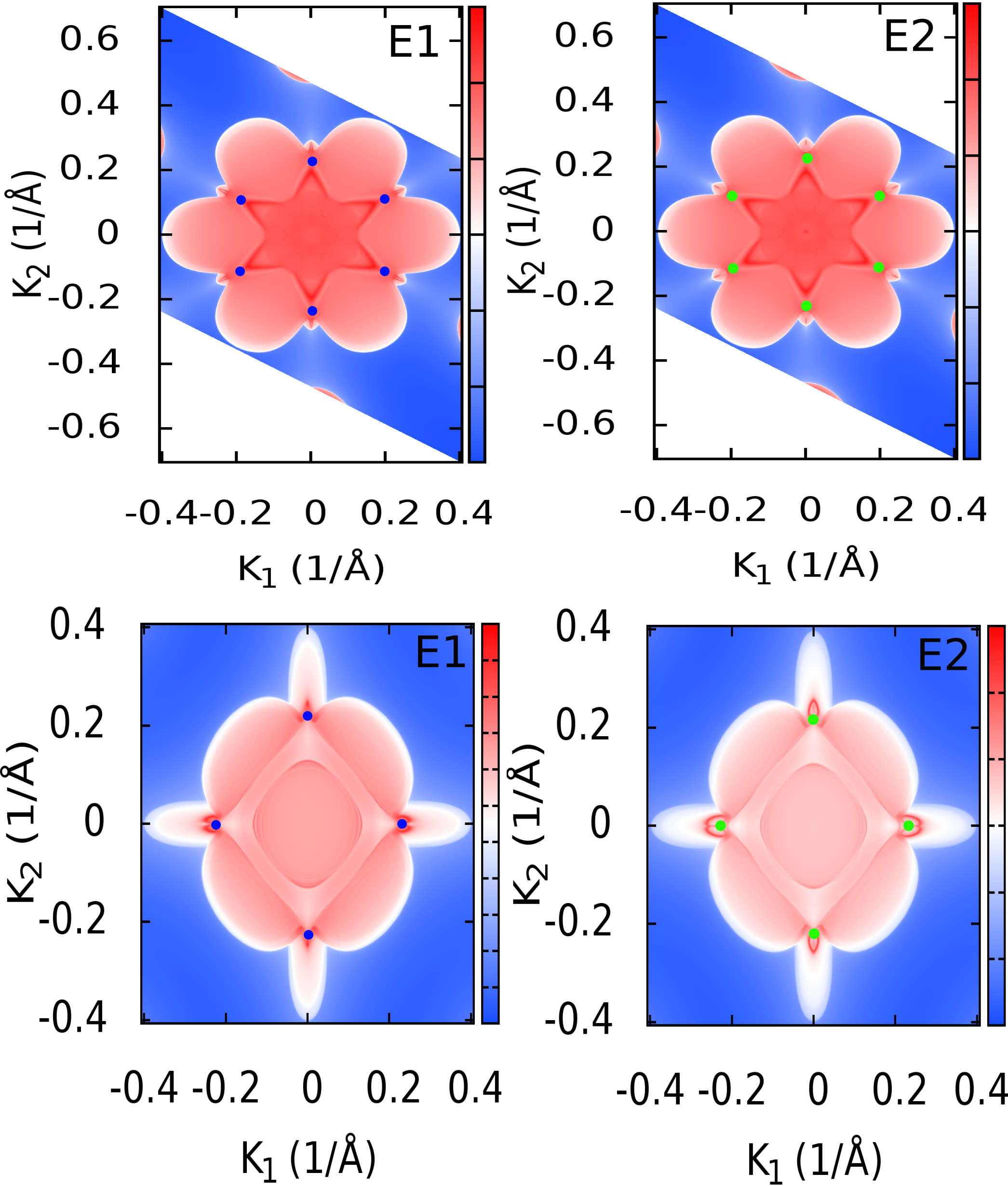
The discovery of quantum materials with nontrivial band topology and robust surface states have garnered significant attention among the scientific community. We theoretically study topological features of quantum materials ranging from topological insulators to semimetals. Topological insulators (TIs) are kind of materials which behave as an insulator in its interior but whose surface contains conducting states, meaning that electrons can only move along the surface of the material. In contrast to TIs, the bulk of certain metals or semimetals are neither boring. Unlike TIs, topological metals and semimetals are interesting not only because of their rich surface physics but also for the exotic nature of linear band crossing in the bulk band structures. Depending on the dimensionality of the band crossing points and Fermi surface topology in the momentum space, distinct topological semimetals have been discovered, namely, Dirac semimetal (DSM), Weyl semimetal (WSM), Nodal line semimetal (NLS), triple point semimetal (TPSM). In NLS, the conduction and the valence bands cross each other along a one-dimensional loop in the three-dimensional Brillouin zone. The DSM and WSM are the low-energy excitations of relativistic Dirac and Weyl fermions with four-fold and two-fold degenerate band crossings, respectively. On the otherhand, TPSM is another class of topological semimetal, which considered to be an intermediate state of Dirac and Weyl semimetal. Unlike DSM and WSM, the band crossing point in TPSM possesses three fold degeneracy. The multi fold band degeneracy in these semimetals are protected by certain crystalline symmetries. 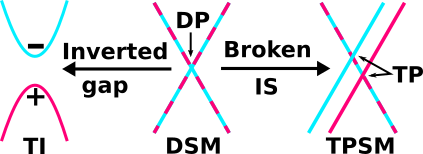Gradual reduction of such symmetries could also lead to have topological phase transition from one to another. Cartoon diagram shows an schematic of DSM, TPSM and gaped phase with an inverted band gap.

Probable kind of systems :

1. Full Heusler alloys, ternary SrAgAs and their families, PtSe2 class, Cd3As2, Na3Bi, elemental metal Ru, Os, Re are few examples of well studied Dirac semimetals.
2. Quaternary and half-Heusler alloys, MoP, WC, NaCu3Te2, RuOs, etc. are few potential class which host triple point Fermions.
3. Magnetic and half Heusler (Co2TiSn, GdPtBi, LiAlGe, Mn2CoSn etc.) are well know materials for Weyl semimetallic phases. Binary CoGe, CoSi, RhSi, SnRh are newly studied Weyl semimetals with long standing Fermi arcs.
4. There are plethora of potential candidates for topological insulators whcih includes antiperovskites (Ba3BiN, Ba3BiP, Ca3BiN etc.), perovskites (KBiO3, BaBiO3 etc.), Heuslers (ZrIrBi, LuPtBi, LaPtBi etc. ), tetradymites (Bi2Se3, Bi2Te3, Sb2Te3, Bi2TexSe1-x etc.) etc.

                      Phys. Rev. B 98, 245149 (2018)